We study the existence and multiplicity of solutions of the problem
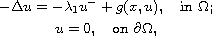
where
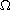 is a smooth bounded domain in
is a smooth bounded domain in
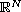
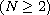 ,
,
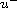 denotes the negative part of
denotes the negative part of
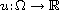 ,
,
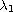 is
the first eigenvalue of the N-dimensional Laplacian with Dirichlet
boundary conditions in
is
the first eigenvalue of the N-dimensional Laplacian with Dirichlet
boundary conditions in
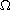 ,
and
,
and
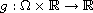 is a continuous function with
is a continuous function with
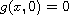 for all
for all
 .
We assume that the nonlinearity g(x,s) has a strong resonant behavior
for large negative values of s and is superlinear, but subcritical,
for large positive values of s. Because of the lack of compactness
in this kind of problem, we establish conditions under which the associated
energy functional satisfies the Palais-Smale condition. We prove the
existence of three nontrivial solutions of the problem as a
consequence of Ekeland's Variational Principle and a variant of the mountain
pass theorem due to Pucci and Serrin [14].
.
We assume that the nonlinearity g(x,s) has a strong resonant behavior
for large negative values of s and is superlinear, but subcritical,
for large positive values of s. Because of the lack of compactness
in this kind of problem, we establish conditions under which the associated
energy functional satisfies the Palais-Smale condition. We prove the
existence of three nontrivial solutions of the problem as a
consequence of Ekeland's Variational Principle and a variant of the mountain
pass theorem due to Pucci and Serrin [14].

