Let X be a real reflexive Banach space and
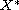 its dual space.
Let
its dual space.
Let
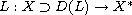 be a densely defined linear maximal
monotone operator, and
be a densely defined linear maximal
monotone operator, and
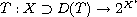 ,
,
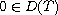 and
and
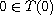 ,
be strongly quasibounded maximal monotone and positively
homogeneous of degree 1. Also, let
,
be strongly quasibounded maximal monotone and positively
homogeneous of degree 1. Also, let
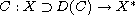 be bounded,
demicontinuous and of type
be bounded,
demicontinuous and of type
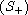 w.r.t. to D(L).
The existence of nonzero solutions of
w.r.t. to D(L).
The existence of nonzero solutions of
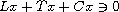 is established
in the set
is established
in the set
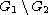 ,
where
,
where
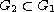 with
with
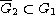 ,
,
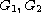 are open sets in X,
are open sets in X,
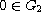 ,
and
,
and
 is bounded. In the special case when L=0, a mapping
is bounded. In the special case when L=0, a mapping
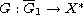 of class (P) introduced by Hu and Papageorgiou
is also incorporated and the existence of nonzero solutions of
of class (P) introduced by Hu and Papageorgiou
is also incorporated and the existence of nonzero solutions of
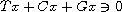 ,
where T is only maximal monotone and positively
homogeneous of degree
,
where T is only maximal monotone and positively
homogeneous of degree
![$\alpha\in (0, 1]$](gifs/aq.gif) ,
is obtained. Applications to
elliptic partial differential equations involving p-Laplacian with
,
is obtained. Applications to
elliptic partial differential equations involving p-Laplacian with
![$p \in (1, 2]$](gifs/ar.gif) and time-dependent parabolic partial differential equations
on cylindrical domains are presented.
and time-dependent parabolic partial differential equations
on cylindrical domains are presented.
 .
.
