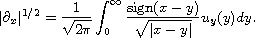Electron. J. Differential Equations,
Vol. 2017 (2017), No. 157, pp. 1-16.
Asymptotic behavior for Dirichlet problems of nonlinear Schrodinger equations
with Landau damping on a half line
Liliana Esquivel
Abstract:
This article is a continuation of the study in [5],
where we proved the existence of solutions, global in time,
for the initial-boundary value problem
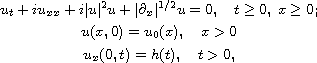
where
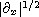 is the module-fractional derivative
operator defined by the modified Riesz Potential
is the module-fractional derivative
operator defined by the modified Riesz Potential
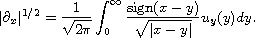
Here, we study the asymptotic behavior of the solution.
Submitted March 6, 2017. Published June 28, 2017.
Math Subject Classifications: 35Q55, 35B40.
Key Words: Fractional Schrodinger equation; boundary value; Landau damping.
Show me the PDF file (285 KB),
TEX file for this article.
 |
Liliana Esquivel
Universidad de Pamplona
Santander, Colombia
email: lesquivel@unipamplona.edu.co
|
|---|
Return to the EJDE web page
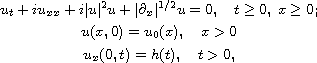
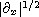 is the module-fractional derivative
operator defined by the modified Riesz Potential
is the module-fractional derivative
operator defined by the modified Riesz Potential