Electron. J. Differential Equations,
Vol. 2017 (2017), No. 185, pp. 1-9.
Existence of solutions to (2,p)-Laplacian equations by Morse theory
Zhanping Liang, Yuanmin Song, Jiabao Su
Abstract:
In this article, we use Morse theory to investigate a type of Dirichlet
boundary value problem related to the (2,p)-Laplacian operator,
where the nonlinear term is characterized by the first eigenvalue of
the Laplace operator. The investigation is heavily based on a new
decomposition about the Banach space
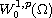 ,
where
,
where
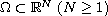 is a bounded domain with smooth
enough boundary.
is a bounded domain with smooth
enough boundary.
Submitted September 26, 2016. Published July 21, 2017.
Math Subject Classifications: 35J50, 35J92, 58E05.
Key Words: (2,p)-Laplacian equation; Morse theory.
Show me the PDF file (229 KB),
TEX file for this article.
 |
Zhanping Liang
School of Mathematical Sciences
Shanxi University
Taiyuan 030006, Shanxi, China
email: lzp@sxu.edu.cn
|
|---|
| |
Yuanmin Song
School of Mathematical Sciences
Shanxi University
Taiyuan 030006, Shanxi, China
email: 954126769@qq.com
|
|---|
| |
Jiabao Su
School of Mathematical Sciences
Capital Normal University
Beijing 100048, China
email: sujb@cnu.edu.cn
|
|---|
Return to the EJDE web page
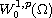 ,
where
,
where
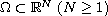 is a bounded domain with smooth
enough boundary.
is a bounded domain with smooth
enough boundary.
