Electron. J. Differential Equations, Vol. 2017 (2017), No. 203, pp. 1-15.

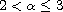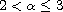Lyapunov-type inequalities for $\alpha$-th order fractional differential equations with $2<\alpha\leq 3$ and fractional boundary conditions

Sougata Dhar, Qingkai Kong

Abstract:
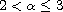We study linear fractional boundary value problems consisting of an $\alpha$-th order Riemann-Liouville fractional differential equation with $2<\alpha\leq 3$ and certain fractional boundary conditions. We derive several Lyapunov-type inequalities and apply them to establish nonexistence, uniqueness, and existence-uniqueness of solutions for related homogeneous and nonhomogeneous linear fractional boundary value problems. As a special case, our work extends some existing results for third-order linear boundary value problems.

Submitted June 2, 2017. Published September 6, 2017.
Math Subject Classifications: 34A08, 34A40, 26A33, 34B05.
Key Words: Fractional differential equations; fractional boundary conditions; Lyapunov-type inequalities; boundary value problems; existence and uniqueness of solutions.

Show me the PDF file (258 KB), TEX file for this article.

Sougata Dhar
Department of Mathematics and Statistics
University of Maine
Orono, ME 04469, USA
email: sougata.dhar@maine.edu
Qingkai Kong
Department of Mathematics
Northern Illinois University
DeKalb, IL 60115, USA
email: qkong@niu.edu

Return to the EJDE web page