In this article we discuss the existence, uniqueness and regularity of solutions of the following system of coupled semilinear Poisson equations on a smooth bounded domain
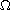 in
in
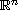 :
:
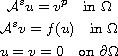
where
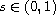 and
and
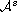 denote spectral fractional
Laplace operators. We assume that
denote spectral fractional
Laplace operators. We assume that
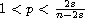 , and the function
f is superlinear and with no growth restriction (for example
, and the function
f is superlinear and with no growth restriction (for example
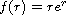 );
thus the system has a nontrivial solution. Another important example is given
by
);
thus the system has a nontrivial solution. Another important example is given
by
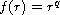 .
In this case, we prove that such a system admits at least one
positive solution for a certain set of the couple (p,q) below the critical
hyperbola
.
In this case, we prove that such a system admits at least one
positive solution for a certain set of the couple (p,q) below the critical
hyperbola
