Electron. J. Differential Equations,
Vol. 2017 (2017), No. 207, pp. 1-10.
Solutions to polytropic filtration equations with a convection term
Huashui Zhan
Abstract:
We introduce a new type of the weak solution of the polytropic
filtration equations with a convection term,
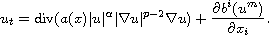
Here,
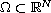 is a domain with a
is a domain with a
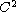 smooth boundary
smooth boundary
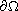 ,
,
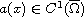 ,
,
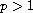 ,
,
 ,
,
 ,
,
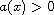 when
when
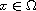 and
and
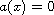 when
when
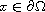 . Since the equation is degenerate on
the boundary, its weak solutions may lack the needed regularity to have a
trace on the boundary. The main aim of the paper is to establish the
stability of the weak solution without any boundary value condition.
. Since the equation is degenerate on
the boundary, its weak solutions may lack the needed regularity to have a
trace on the boundary. The main aim of the paper is to establish the
stability of the weak solution without any boundary value condition.
Submitted February 16, 2017. Published September 8, 2017.
Math Subject Classifications: 35L65, 35K85, 35R35.
Key Words: Polytropic filtration equation; convection term; stability;
boundary value condition.
Show me the PDF file (241 KB),
TEX file for this article.
 |
Huashui Zhan
School of Applied Mathematics
Xiamen University of Technology
Xiamen, Fujian 361024, China
email: 2012111007@xmut.edu.cn
|
|---|
Return to the EJDE web page
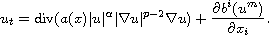
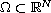 is a domain with a
is a domain with a
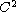 smooth boundary
smooth boundary
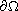 ,
,
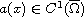 ,
,
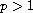 ,
,
 ,
,
 ,
,
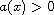 when
when
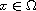 and
and
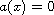 when
when
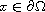 . Since the equation is degenerate on
the boundary, its weak solutions may lack the needed regularity to have a
trace on the boundary. The main aim of the paper is to establish the
stability of the weak solution without any boundary value condition.
. Since the equation is degenerate on
the boundary, its weak solutions may lack the needed regularity to have a
trace on the boundary. The main aim of the paper is to establish the
stability of the weak solution without any boundary value condition.
