Electron. J. Differential Equations,
Vol. 2017 (2017), No. 217, pp. 1-7.
Explicit limit cycles of a family of polynomial differential systems
Rachid Boukoucha
Abstract:
We consider the family of polynomial differential systems
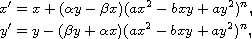
where a, b,
 ,
,
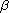 are real constants and n is positive
integer. We prove that these systems are Liouville integrable. Moreover, we
determine sufficient conditions for the existence of an explicit algebraic or
non-algebraic limit cycle. Examples exhibiting the applicability of our
result are introduced.
are real constants and n is positive
integer. We prove that these systems are Liouville integrable. Moreover, we
determine sufficient conditions for the existence of an explicit algebraic or
non-algebraic limit cycle. Examples exhibiting the applicability of our
result are introduced.
Submitted October 4, 2016. Published September 13, 2017.
Math Subject Classifications: 34A05, 34C05, 34CO7, 34C25.
Key Words: Planar polynomial differential system; first integral;
Algebraic limit cycle; non-algebraic limit cycle.
Show me the PDF file (199 KB),
TEX file for this article.
 |
Rachid Boukoucha
Department of Technology
Faculty of Technology
University of Bejaia
06000 Bejaia, Algeria
email: rachid_boukecha@yahoo.fr
|
|---|
Return to the EJDE web page
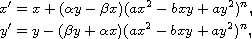
 ,
,
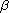 are real constants and n is positive
integer. We prove that these systems are Liouville integrable. Moreover, we
determine sufficient conditions for the existence of an explicit algebraic or
non-algebraic limit cycle. Examples exhibiting the applicability of our
result are introduced.
are real constants and n is positive
integer. We prove that these systems are Liouville integrable. Moreover, we
determine sufficient conditions for the existence of an explicit algebraic or
non-algebraic limit cycle. Examples exhibiting the applicability of our
result are introduced.
