Electron. J. Differential Equations,
Vol. 2017 (2017), No. 228, pp. 1-12.
Sequences of small homoclinic solutions for difference equations
on integers
Robert Steglinski
Abstract:
In this article, we determine a concrete interval of positive parameters
 ,
for which we prove the existence of infinitely many homoclinic
solutions for a discrete problem
,
for which we prove the existence of infinitely many homoclinic
solutions for a discrete problem
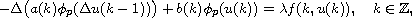
where the nonlinear term
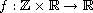 has an appropriate oscillatory behavior at zero. We use both the general
variational principle of Ricceri and the direct method introduced by
Faraci and Kristaly [11].
has an appropriate oscillatory behavior at zero. We use both the general
variational principle of Ricceri and the direct method introduced by
Faraci and Kristaly [11].
Submitted July 18, 2017. Published September 22, 2017.
Math Subject Classifications: 39A10, 47J30, 35B38.
Key Words: Difference equations; discrete p-Laplacian; variational methods;
infinitely many solutions.
Show me the PDF file (270 KB),
TEX file for this article.
 |
Robert Steglinski
Institute of Mathematics
Lodz University of Technology
Wolczanska 215, 90-924 Lodz, Poland
email: robert.steglinski@p.lodz.pl
|
|---|
Return to the EJDE web page
 ,
for which we prove the existence of infinitely many homoclinic
solutions for a discrete problem
,
for which we prove the existence of infinitely many homoclinic
solutions for a discrete problem
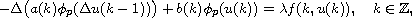
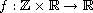 has an appropriate oscillatory behavior at zero. We use both the general
variational principle of Ricceri and the direct method introduced by
Faraci and Kristaly [11].
has an appropriate oscillatory behavior at zero. We use both the general
variational principle of Ricceri and the direct method introduced by
Faraci and Kristaly [11].
