Electron. J. Differential Equations,
Vol. 2017 (2017), No. 23, pp. 1-16.
On a reaction-diffusion system associated with brain lactate kinetics
Remy Guillevin, Alain Miranville, Angelique Perrillat-Mercerot
Abstract:
Our aim in this article is to study properties of a reaction-diffusion
system which is related with brain lactate kinetics, when spatial diffusion
is taken into account. In particular, we prove the existence and uniqueness
of nonnegative solutions and obtain linear stability results. We also derive
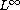 -bounds
on the solutions. These results give insights on the
therapeutic management of glioma.
-bounds
on the solutions. These results give insights on the
therapeutic management of glioma.
Submitted November 18, 2016. Published January 18, 2017.
Math Subject Classifications: 35K57, 35K67, 35B45.
Key Words: Brain lactate kinetics; spatial diffusion; reaction-diffusion system;
well-posedness; regularity; linear stability.
Show me the PDF file (276 KB),
TEX file for this article.
Rémy Guillevin
Université de Poitiers
F-86962 Chasseneuil Futuroscope Cedex, France
email: remy.guillevin@chu-poitiers.fr
|
Alain Miranville
Université de Poitiers
F-86962 Chasseneuil Futuroscope Cedex, France
email: alain.miranville@math.univ-poitiers.fr
|
Angélique Perrillat-Mercerot
Université de Poitiers
F-86962 Chasseneuil Futuroscope Cedex, France
email: Angelique.Perrillat@math.univ-poitiers.fr
|
Return to the EJDE web page
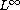 -bounds
on the solutions. These results give insights on the
therapeutic management of glioma.
-bounds
on the solutions. These results give insights on the
therapeutic management of glioma.