Electron. J. Differential Equations,
Vol. 2017 (2017), No. 230, pp. 1-17.
Existence of infinitely many solutions for degenerate
Kirchhoff-type Schrodinger-Choquard equations
Sihua Liang, Vicentiu D. Radulescu
Abstract:
In this article we study a class of Kirchhoff-type
Schrodinger-Choquard equations involving the
fractional p-Laplacian. By means of Kajikiya's new version of
the symmetric mountain pass lemma, we obtain the existence of
infinitely many solutions which tend to zero under a suitable value
of
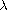 .
The main feature and difficulty of our equations arise
in the fact that the Kirchhoff term M could vanish at zero, that is,
the problem is degenerate. To our best knowledge, our result
is new even in the framework of Schrodinger-Choquard problems.
.
The main feature and difficulty of our equations arise
in the fact that the Kirchhoff term M could vanish at zero, that is,
the problem is degenerate. To our best knowledge, our result
is new even in the framework of Schrodinger-Choquard problems.
Submitted July 10, 2017. Published September 22, 2017.
Math Subject Classifications: 35R11, 35A15, 47G20.
Key Words: Kirchhoff-type problems; Schrodinger-Choquard equations;
fractional p-Laplacian; critical exponent; variational methods.
Show me the PDF file (311 KB),
TEX file for this article.
 |
Sihua Liang
College of Mathematics
Changchun Normal University
Changchun 130032, Jilin, China
email: liangsihua@126.com
|
|---|
 |
Vicentiu D. Radulescu
Department of Mathematics, Faculty of Sciences
King Abdulaziz University, P.O. Box 80203
Jeddah 21589, Saudi Arabia
email: vicentiu.radulescu@imar.ro
|
|---|
Return to the EJDE web page
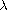 .
The main feature and difficulty of our equations arise
in the fact that the Kirchhoff term M could vanish at zero, that is,
the problem is degenerate. To our best knowledge, our result
is new even in the framework of Schrodinger-Choquard problems.
.
The main feature and difficulty of our equations arise
in the fact that the Kirchhoff term M could vanish at zero, that is,
the problem is degenerate. To our best knowledge, our result
is new even in the framework of Schrodinger-Choquard problems.

