Electron. J. Differential Equations,
Vol. 2017 (2017), No. 244, pp. 1-11.
Time-periodic strong solutions of the 3D Navier-Stokes equations with damping
Yongho Kim, Kwangok Li
Abstract:
This article concerns the incompressible Navier-Stokes equations with
damping and homogeneous Dirichlet boundary conditions in 3D bounded domains.
We find conditions on parameters to guarantee that the problem has a
strong time-periodic solution and that the weak solutions of the problem
converge to a unique time-periodic solution as
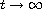 .
.
Submitted May 16, 2017. Published October 5, 2017.
Math Subject Classifications: 35Q30, 76D05.
Key Words: 3D Navier-Stokes equation; asymptotic behavior; nonlinear damping;
time-periodic solution.
Show me the PDF file (220 KB),
TEX file for this article.
 |
Yongho Kim
Department of Mathematics
University of Science
Pyongyang, DPR Korea
email: kyho555@star-co.net.kp
|
|---|
 |
Kwangok Li
Department of Mathematics
University of Science
Pyongyang, DPR Korea
email: liko@star-co.net.kp
|
|---|
Return to the EJDE web page
 .
.

