Electron. J. Differential Equations,
Vol. 2017 (2017), No. 254, pp. 1-9.
Existence and asymptotic behavior of global solutions
to chemorepulsion systems with nonlinear sensitivity
Yulin Lai, Youjun Xiao
Abstract:
This article concerns the chemorepulsion system with nonlinear
sensitivity and nonlinear secretion

under homogeneous Neumann boundary conditions, where
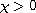 ,
m>0,
,
m>0,
 ,
,
 is a bounded domain with
smooth boundary. The existence and uniform boundedness of a
classical global solutions are obtained. Furthermore, it is shown that
for any given
is a bounded domain with
smooth boundary. The existence and uniform boundedness of a
classical global solutions are obtained. Furthermore, it is shown that
for any given
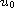 , if
, if
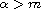 or
or
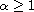 ,
the corresponding
solution (u,v) converges to
,
the corresponding
solution (u,v) converges to
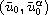 as time
goes to infinity, where
as time
goes to infinity, where
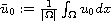 .
.
Submitted April 7, 2017. Published October 10, 2017.
Math Subject Classifications: 35K55, 35Q92, 35Q35, 92C17.
Key Words: Chemotaxis; repulsion; nonlinear sensitivity;global solution;
asymptotic behavior.
Show me the PDF file (240 KB),
TEX file for this article.
 |
Yulin Lai
Third People's Hospital of Yibin City
Yibin 644000, China
email: 32212779@qq.com
|
|---|
 |
Youjun Xiao
College of Mathematic & Information
China West Normal University
Nanchong 637002, China
email: mathxyj@126.com
|
|---|
Return to the EJDE web page

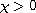 ,
m>0,
,
m>0,
 ,
,
 is a bounded domain with
smooth boundary. The existence and uniform boundedness of a
classical global solutions are obtained. Furthermore, it is shown that
for any given
is a bounded domain with
smooth boundary. The existence and uniform boundedness of a
classical global solutions are obtained. Furthermore, it is shown that
for any given
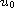 , if
, if
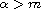 or
or
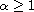 ,
the corresponding
solution (u,v) converges to
,
the corresponding
solution (u,v) converges to
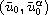 as time
goes to infinity, where
as time
goes to infinity, where
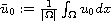 .
.

