We consider a model mixing sharp and diffuse interface approaches for seawater intrusion phenomenons in confined and unconfined aquifers. More precisely, a phase field model is introduced in the boundary conditions on the virtual sharp interfaces. We thus include in the model the existence of diffuse transition zones but we preserve the simplified structure allowing front tracking. The three-dimensional problem then reduces to a two-dimensional model involving a strongly coupled system of partial differential equations of parabolic and elliptic type describing the evolution of the depth of the interface between salt- and freshwater and the evolution of the freshwater hydraulic head. Assuming a low hydraulic conductivity inside the aquifer, we prove the uniqueness of a weak solution for the model completed with initial and boundary conditions. Thanks to a generalization of a Meyer's regularity result, we establish that the gradient of the solution belongs to the space
,
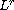r>2. This additional regularity combined with the Gagliardo-Nirenberg
inequality for r=4 allows to handle the nonlinearity of the system in
the proof of uniqueness.
