This article concerns the nonlinear wave equation

Essentially this article ascertains and proves the important mapping property

as well as the associated Lipschitz condition
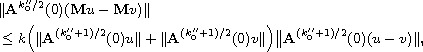
where
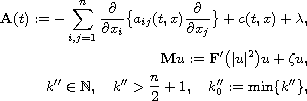
and
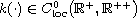 is monotonically increasing. Here are
is monotonically increasing. Here are
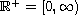 ,
,
 .
This mapping property is true for the dimensions
.
This mapping property is true for the dimensions
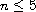 .
But we investigate only the case
.
But we investigate only the case
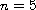 because the problem is already
solved for
because the problem is already
solved for
 ,
however, without the mapping property.
With the proof of the mapping property and the associated Lipschitz condition,
the problem becomes considerably comparable with a paper from von Wahl,
who investigated the same problem as Cauchy problem and solved it for
the dimensions
,
however, without the mapping property.
With the proof of the mapping property and the associated Lipschitz condition,
the problem becomes considerably comparable with a paper from von Wahl,
who investigated the same problem as Cauchy problem and solved it for
the dimensions
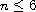 ,
i.e. without boundary condition.
In the case of the Cauchy problem there are no difficulties with regard
to the mapping property.
,
i.e. without boundary condition.
In the case of the Cauchy problem there are no difficulties with regard
to the mapping property.
