Electron. J. Differential Equations,
Vol. 2017 (2017), No. 284, pp. 1-8.
Regularity lifting result for an integral system involving
Riesz potentials
Yayun Li, Deyun Xu
Abstract:
In this article, we study the integral system involving the Riesz potentials
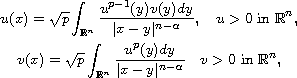
where
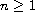 ,
,
 and
and
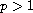 .
Such a system is related
to the study of a static Hartree equation and the Hardy-Littlewood-Sobolev
inequality. We investigate the regularity of positive solutions
and prove that some integrable solutions belong to
.
Such a system is related
to the study of a static Hartree equation and the Hardy-Littlewood-Sobolev
inequality. We investigate the regularity of positive solutions
and prove that some integrable solutions belong to
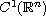 . An
essential regularity lifting lemma comes into play, which was
established by Chen, Li and Ma [20].
. An
essential regularity lifting lemma comes into play, which was
established by Chen, Li and Ma [20].
Submitted May 16, 2017. Published November 14, 2017.
Math Subject Classifications: 35J10, 35Q55, 45E10, 45G05.
Key Words: Riesz potential; integral system; regularity lifting lemma;
Hartree equation; Hardy-Littlewood-Sobolev inequality.
Show me the PDF file (218 KB),
TEX file for this article.
 |
Yayun Li
Institute of Mathematics
School of Mathematical Sciences
Nanjing Normal University
Nanjing, 210023, China
email: liyayun.njnu@qq.com
|
|---|
| |
Deyun Xu
Institute of Mathematics
School of Mathematical Sciences
Nanjing Normal University
Nanjing, 210023, China
email: 954816700@qq.com
|
|---|
Return to the EJDE web page
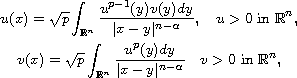
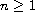 ,
,
 and
and
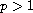 .
Such a system is related
to the study of a static Hartree equation and the Hardy-Littlewood-Sobolev
inequality. We investigate the regularity of positive solutions
and prove that some integrable solutions belong to
.
Such a system is related
to the study of a static Hartree equation and the Hardy-Littlewood-Sobolev
inequality. We investigate the regularity of positive solutions
and prove that some integrable solutions belong to
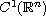 . An
essential regularity lifting lemma comes into play, which was
established by Chen, Li and Ma [20].
. An
essential regularity lifting lemma comes into play, which was
established by Chen, Li and Ma [20].
