Let QSH be the whole class of non-degenerate planar quadratic differential systems possessing at least one invariant hyperbola. We classify this family of systems, modulo the action of the group of real affine transformations and time rescaling, according to their geometric properties encoded in the configurations of invariant hyperbolas and invariant straight lines which these systems possess. The classification is given both in terms of algebraic geometric invariants and also in terms of affine invariant polynomials. It yields a total of 205 distinct such configurations. We have 162 configurations for the subclass QSH
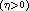 of systems which possess three
distinct real singularities at infinity in
of systems which possess three
distinct real singularities at infinity in
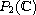 ,
and 43 configurations for the subclass QSH
,
and 43 configurations for the subclass QSH
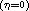 of systems
which possess either exactly two distinct real singularities at
infinity or the line at infinity filled up with singularities.
The algebraic classification, based on the invariant polynomials,
is also an algorithm which makes it possible to verify for any given
real quadratic differential system if it has invariant hyperbolas or
not and to specify its configuration of invariant hyperbolas and
straight lines.
of systems
which possess either exactly two distinct real singularities at
infinity or the line at infinity filled up with singularities.
The algebraic classification, based on the invariant polynomials,
is also an algorithm which makes it possible to verify for any given
real quadratic differential system if it has invariant hyperbolas or
not and to specify its configuration of invariant hyperbolas and
straight lines.



