Electron. J. Differential Equations,
Vol. 2017 (2017), No. 307, pp. 1-11.
Spectral properties of a fourth-order eigenvalue problem with
spectral parameter in the boundary conditions
Ziyatkhan S. Aliyev, Faiq M. Namazov
Abstract:
In this article we consider eigenvalue problems for fourth-order
ordinary differential equation with spectral parameter in boundary
conditions. We study the location of eigenvalues on the real axis,
find the multiplicities of eigenvalues, investigate the oscillation
properties of eigenfunctions, and the basis properties in the space
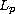 ,
,
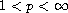 , of the subsystems of eigenfunctions of this
problem.
, of the subsystems of eigenfunctions of this
problem.
Submitted August 29, 2017. Published December 14, 2017.
Math Subject Classifications: 34B05, 34B09, 34B24.
Key Words: Bending vibrations of a homogeneous rod; fourth order ODE;
oscillation properties of eigenfunctions;
basis properties of eigenfunctions.
Show me the PDF file (268 KB),
TEX file for this article.
 |
Ziyatkhan S. Aliyev
Baku State University
Baku AZ1148, Azerbaijan
email: z_aliyev@mail.ru
|
|---|
 |
Faiq M. Namazov
Baku State University
Baku AZ1148, Azerbaijan
email: faig-namazov@mail.ru
|
|---|
Return to the EJDE web page
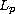 ,
,
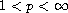 , of the subsystems of eigenfunctions of this
problem.
, of the subsystems of eigenfunctions of this
problem.

