Using Leray-Schauder degree theory and the method of upper and lower solutions, we obtain a solution for nonlinear boundary-value problem
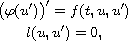
where l(u,u')=0 denotes the three-point boundary conditions on [0,T], and
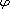 is a homeomorphism such that
is a homeomorphism such that
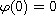 .
.
Dionicio Pastor Dallos Santos
Abstract:
Using Leray-Schauder degree theory and the method of upper and lower solutions,
we obtain a solution for nonlinear boundary-value problem
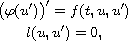
where l(u,u')=0 denotes the three-point boundary conditions on
[0,T], and
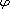 is a homeomorphism such that
is a homeomorphism such that
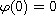 .
.
Submitted September 21, 2016. Published January 30, 2017.
Math Subject Classifications: 34B15, 34B16, 47H10, 47H11.
Key Words: Boundary value problems; Schauder fixed point theorem;
Leray-Schauder degree; lower and upper solutions.
Show me the PDF file (221 KB), TEX file for this article.
 |
Dionicio Pastor Dallos Santos Department of Mathematics, IME-USP Cidade Universitária CEP 05508-090, São Paulo, SP, Brazil email: dionicio@ime.usp.br |
|---|
Return to the EJDE web page