Electron. J. Differential Equations,
Vol. 2017 (2017), No. 44, pp. 1-12.
Moving-boundary problems for the time-fractional
diffusion equation
Sabrina D. Roscani
Abstract:
We consider a one-dimensional moving-boundary problem
for the time-fractional diffusion equation. The time-fractional derivative
of order
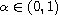 is taken in the sense of Caputo.
We study the asymptotic behaivor, as t tends to infinity, of a
general solution by using a fractional weak maximum principle.
Also, we give some particular exact solutions in terms of Wright functions.
is taken in the sense of Caputo.
We study the asymptotic behaivor, as t tends to infinity, of a
general solution by using a fractional weak maximum principle.
Also, we give some particular exact solutions in terms of Wright functions.
Submitted August 26, 2016. Published February 14, 2017.
Math Subject Classifications: 26A33, 35R37, 33E12, 33E20.
Key Words: Fractional diffusion equation; Caputo derivative;
moving-boundary problem; maximum principle; asymptotic behaivor.
Show me the PDF file (248 KB),
TEX file for this article.
 |
Sabrina D. Roscani
CONICET - Departamento de Matemática FCE
Universidad Austral, Paraguay 1950
S2000FZF Rosario, Argentina
email: sabrinaroscani@gmail.com
|
|---|
Return to the EJDE web page
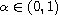 is taken in the sense of Caputo.
We study the asymptotic behaivor, as t tends to infinity, of a
general solution by using a fractional weak maximum principle.
Also, we give some particular exact solutions in terms of Wright functions.
is taken in the sense of Caputo.
We study the asymptotic behaivor, as t tends to infinity, of a
general solution by using a fractional weak maximum principle.
Also, we give some particular exact solutions in terms of Wright functions.
