Electron. J. Differential Equations,
Vol. 2017 (2017), No. 49, pp. 1-17.
Characterization of a homogeneous Orlicz space
Waldo Arriagada, Jorge Huentutripay
Abstract:
In this article we define and characterize the homogeneous Orlicz space
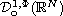 where
where
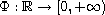 is the N-function generated by an odd, increasing and not-necessarily
differentiable homeomorphism
is the N-function generated by an odd, increasing and not-necessarily
differentiable homeomorphism
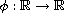 .
The properties of
.
The properties of
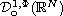 are treated
in connection with the
are treated
in connection with the
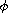 -Laplacian
eigenvalue problem
-Laplacian
eigenvalue problem
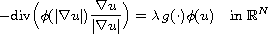
where
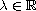 and
and
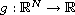 is measurable.
We use a classic Lagrange rule to prove that solutions of the
is measurable.
We use a classic Lagrange rule to prove that solutions of the
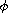 -Laplace
operator exist and are non-negative.
-Laplace
operator exist and are non-negative.
Submitted August 31, 2016. Published February 16, 2017.
Math Subject Classifications: 46E30, 46T30, 35J20, 35J50.
Key Words: Homogeneous space; Orlicz space; eigenvalue problem; phi-Laplacian
Show me the PDF file (320 KB),
TEX file for this article.
 |
Waldo Arriagada
Department of Applied Mathematics and Sciences
Khalifa University, Al Zafranah, P.O. Box 127788
Abu Dhabi, United Arab Emirates
email: waldo.arriagada@kustar.ac.ae
|
|---|
 |
Jorge Huentutripay
Instituto de Ciencias Físicas y Matemáticas
Universidad Austral de Chile
Casilla 567, Valdivia, Chile
email: jorge.huentutripay@uach.cl
|
|---|
Return to the EJDE web page
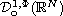 where
where
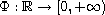 is the N-function generated by an odd, increasing and not-necessarily
differentiable homeomorphism
is the N-function generated by an odd, increasing and not-necessarily
differentiable homeomorphism
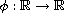 .
The properties of
.
The properties of
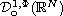 are treated
in connection with the
are treated
in connection with the
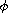 -Laplacian
eigenvalue problem
-Laplacian
eigenvalue problem
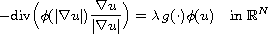
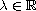 and
and
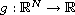 is measurable.
We use a classic Lagrange rule to prove that solutions of the
is measurable.
We use a classic Lagrange rule to prove that solutions of the
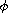 -Laplace
operator exist and are non-negative.
-Laplace
operator exist and are non-negative.

