Electron. J. Differential Equations,
Vol. 2017 (2017), No. 76, pp. 1-10.
Existence of standing waves for Schrodinger equations involving
the fractional Laplacian
Everaldo S. de Medeiros, Jose Anderson Cardoso, Manasses de Souza
Abstract:
We study a class of fractional Schrodinger equations of the form
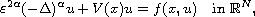
where
 is a positive parameter,
is a positive parameter,
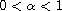 ,
,
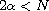 ,
,
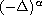 is the fractional Laplacian,
is the fractional Laplacian,
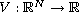 is a potential which may be
bounded or unbounded and the nonlinearity
is a potential which may be
bounded or unbounded and the nonlinearity
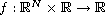 is superlinear and
behaves like
is superlinear and
behaves like
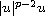 at infinity for some
at infinity for some
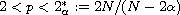 .
Here we use a variational approach based on the Caffarelli and Silvestre's
extension developed in [3] to obtain a nontrivial solution
for
.
Here we use a variational approach based on the Caffarelli and Silvestre's
extension developed in [3] to obtain a nontrivial solution
for
 sufficiently small.
sufficiently small.
Submitted September 16, 2016. Published March 20, 2017.
Math Subject Classifications: 35J20, 35J60, 35R11.
Key Words: Variational methods; critical points; fractional Laplacian.
Show me the PDF file (255 KB),
TEX file for this article.
 |
Everaldo S. de Medeiros
Departamento de Matemática
Universidade Federal da Paraíba, 58051-900
João Pessoa, PB, Brazil
email: everaldomedeiros1@gmail.com
|
|---|
 |
Jose Anderson Cardoso
Departamento de Matemática
Universidade Federal de Sergipe, 49000-100
São Cristóvão, Brazil
email: anderson@mat.ufs.br
|
|---|
 |
Manassés de Souza
Departamento de Matemática
Universidade Federal da Paraíba, 58051-900
João Pessoa, PB, Brazil
email: manassesxavier@gmail.com
|
|---|
Return to the EJDE web page
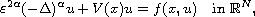
 is a positive parameter,
is a positive parameter,
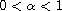 ,
,
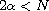 ,
,
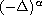 is the fractional Laplacian,
is the fractional Laplacian,
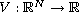 is a potential which may be
bounded or unbounded and the nonlinearity
is a potential which may be
bounded or unbounded and the nonlinearity
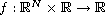 is superlinear and
behaves like
is superlinear and
behaves like
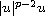 at infinity for some
at infinity for some
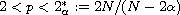 .
Here we use a variational approach based on the Caffarelli and Silvestre's
extension developed in [3] to obtain a nontrivial solution
for
.
Here we use a variational approach based on the Caffarelli and Silvestre's
extension developed in [3] to obtain a nontrivial solution
for
 sufficiently small.
sufficiently small.


