Electron. J. Differential Equations,
Vol. 2017 (2017), No. 77, pp. 1-21.
Nonlinear perturbations of the Kirchhoff equation
Manuel Milla Miranda, Aldo T. Louredo, Luiz A. Medeiros
Abstract:
In this article we study the existence and uniqueness of local solutions
for the initial-boundary value problem for the Kirchhoff equation
![$$\displaylines{
u'' - M(t,\|u(t)\|^{2})\Delta u + |u|^{\rho} =f \quad\text{in }
\Omega \times (0, T_0), \cr
u=0\quad\text{on }\Gamma_0 \times ]0, T_0[, \cr
\frac{\partial u}{\partial \nu} + \delta h(u')=0 \quad\text{on }
\Gamma_1 \times ]0, T_0[,
}$$](gifs/aa.gif)
where
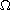 is a bounded domain of
is a bounded domain of
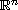 with its boundary
constiting of two disjoint parts
with its boundary
constiting of two disjoint parts
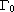 and
and
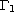 ;
;
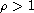 is a real number;
is a real number;
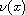 is the exterior unit normal vector at
is the exterior unit normal vector at
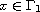 and
and
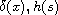 are real functions defined in
are real functions defined in
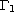 and
and
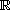 ,
respectively.
Our result is obtained using the Galerkin method with a special basis,
the Tartar argument, the compactness approach, and a Fixed-Point method.
,
respectively.
Our result is obtained using the Galerkin method with a special basis,
the Tartar argument, the compactness approach, and a Fixed-Point method.
Submitted January 24, 2017. Published March 21, 2017.
Math Subject Classifications: 35L15, 35L20, 35K55, 35L60, 35L70.
Key Words: Kirchhoff equation; nonlinear boundary condition;
existence of solutions.
Show me the PDF file (315 KB),
TEX file for this article.
 |
Manuel Milla Miranda
Universidade Estadual da Paraíba
DM, PB, Brazil
email: milla@im.ufrj.br
|
|---|
 |
Aldo T. Louredo
Universidade Estadual da Paraíba
DM, PB, Brazil
email: aldolouredo@gmail.com
Phone: +55 (83) 3315-3340
|
|---|
 |
Luiz A. Medeiros
Universidade Federal do Rio de Janeiro
IM, RJ, Brazil
email: luizadauto@gmail.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
u'' - M(t,\|u(t)\|^{2})\Delta u + |u|^{\rho} =f \quad\text{in }
\Omega \times (0, T_0), \cr
u=0\quad\text{on }\Gamma_0 \times ]0, T_0[, \cr
\frac{\partial u}{\partial \nu} + \delta h(u')=0 \quad\text{on }
\Gamma_1 \times ]0, T_0[,
}$$](gifs/aa.gif)
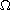 is a bounded domain of
is a bounded domain of
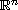 with its boundary
constiting of two disjoint parts
with its boundary
constiting of two disjoint parts
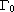 and
and
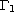 ;
;
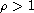 is a real number;
is a real number;
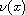 is the exterior unit normal vector at
is the exterior unit normal vector at
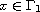 and
and
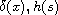 are real functions defined in
are real functions defined in
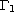 and
and
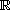 ,
respectively.
Our result is obtained using the Galerkin method with a special basis,
the Tartar argument, the compactness approach, and a Fixed-Point method.
,
respectively.
Our result is obtained using the Galerkin method with a special basis,
the Tartar argument, the compactness approach, and a Fixed-Point method.


