Electron. J. Differential Equations,
Vol. 2018 (2018), No. 03, pp. 1-21.
Asymptotic behavior of pullback attractors for non-autonomous
micropolar fluid flows in 2D unbounded domains
Wenlong Sun, Yeping Li
Abstract:
In this article, we investigate the pullback asymptotic behavior of
solutions for a non-autonomous micropolar fluid flows in 2D unbounded
channel-like domains. First, applying the technique of truncation
functions, decomposition of spatial domain, and the energy method,
we show the existence of the pullback attractor in the space
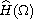 (has L^2-regularity). In fact,
we can deduce the existence of pullback attractor in space
(has L^2-regularity). In fact,
we can deduce the existence of pullback attractor in space
 (has H^1-regularity). Also the tempered behavior
of the pullback attractor is verified. Moreover, when the spatial
domain varies from
(has H^1-regularity). Also the tempered behavior
of the pullback attractor is verified. Moreover, when the spatial
domain varies from
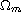 (
(
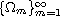 be an
expanding sequence of simply connected, bounded and smooth subdomains
of
be an
expanding sequence of simply connected, bounded and smooth subdomains
of
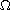 such that
such that
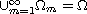 )
to
)
to 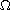 ,
the upper semicontinuity of the pullback attractor is discussed.
,
the upper semicontinuity of the pullback attractor is discussed.
Submitted March 6, 2017. Published January 4, 2018.
Math Subject Classifications: 35B40, 35B41, 35Q30.
Key Words: Micropolar fluid flow; pullback attractor; truncation function;
tempered behavior; upper semicontinuity.
Show me the PDF file (335 KB),
TEX file for this article.
| |
Wenlong Sun
Department of Mathematics
East China University of Science and Technology
Shanghai 200237, China
email: wenlongsun1988@163.com
|
|---|
 |
Yeping Li
Department of Mathematics
East China University of Science and Technology
Shanghai 200237, China
email: yplee@ecust.edu.cn
|
|---|
Return to the EJDE web page
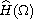 (has L^2-regularity). In fact,
we can deduce the existence of pullback attractor in space
(has L^2-regularity). In fact,
we can deduce the existence of pullback attractor in space
 (has H^1-regularity). Also the tempered behavior
of the pullback attractor is verified. Moreover, when the spatial
domain varies from
(has H^1-regularity). Also the tempered behavior
of the pullback attractor is verified. Moreover, when the spatial
domain varies from
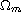 (
(
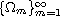 be an
expanding sequence of simply connected, bounded and smooth subdomains
of
be an
expanding sequence of simply connected, bounded and smooth subdomains
of
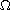 such that
such that
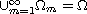 )
to
)
to 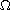 ,
the upper semicontinuity of the pullback attractor is discussed.
,
the upper semicontinuity of the pullback attractor is discussed.
