Electron. J. Differential Equations,
Vol. 2018 (2018), No. 07, pp. 1-9.
Uniform stability of the ball with respect to the first Dirichlet and Neumann
infinity-eigenvalues
Joao Vitor da Silva, Julio D. Rossi, Ariel M. Salort
Abstract:
In this note we analyze how perturbations of a ball
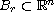 behaves in terms of their first
(non-trivial) Neumann and Dirichlet
behaves in terms of their first
(non-trivial) Neumann and Dirichlet
 -eigenvalues
when a volume
constraint
-eigenvalues
when a volume
constraint
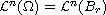 is imposed.
Our main result states that
is imposed.
Our main result states that
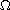 is uniformly close to a ball when
it has first Neumann and Dirichlet eigenvalues close to the ones for the
ball of the same volume
is uniformly close to a ball when
it has first Neumann and Dirichlet eigenvalues close to the ones for the
ball of the same volume
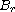 .
In fact, we show that, if
.
In fact, we show that, if
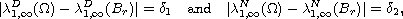
then there are two balls such that
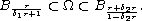
In addition, we obtain a result concerning stability of the Dirichlet
 -eigenfunctions.
-eigenfunctions.
Submitted September 9, 2017. Published January 6, 2018.
Math Subject Classifications: 35B27, 35J60, 35J70.
Key Words: Infinity-eigenvalues estimates; infinity-eigenvalue problem;
approximation of domains.
Show me the PDF file (326 KB),
TEX file for this article.
 |
João Vitor da Silva
Departamento de Matem ática
FCEyN - Universidad de Buenos Aires, Argentina
email: jdasilva@dm.uba.ar
|
|---|
 |
Julio D. Rossi
Departamento de Matem ática
FCEyN - Universidad de Buenos Aires, Argentina
email: jrossi@dm.uba.ar
|
|---|
 |
Ariel M. Salort
Departamento de Matem ática
FCEyN - Universidad de Buenos Aires, Argentina
email: asalort@dm.uba.ar
|
|---|
Return to the EJDE web page
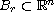 behaves in terms of their first
(non-trivial) Neumann and Dirichlet
behaves in terms of their first
(non-trivial) Neumann and Dirichlet
 -eigenvalues
when a volume
constraint
-eigenvalues
when a volume
constraint
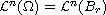 is imposed.
Our main result states that
is imposed.
Our main result states that
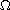 is uniformly close to a ball when
it has first Neumann and Dirichlet eigenvalues close to the ones for the
ball of the same volume
is uniformly close to a ball when
it has first Neumann and Dirichlet eigenvalues close to the ones for the
ball of the same volume
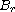 .
In fact, we show that, if
.
In fact, we show that, if
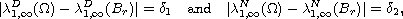
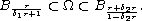
 -eigenfunctions.
-eigenfunctions.


