Let
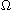 be a bounded q-pseudoconvex domain in
be a bounded q-pseudoconvex domain in
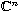 ,
,
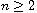 and let
and let
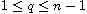 .
If
.
If
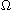 is smooth, we find sufficient conditions for the
is smooth, we find sufficient conditions for the
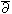 -Neumann operator to be compact.
If
-Neumann operator to be compact.
If
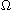 is non-smooth and if
is non-smooth and if
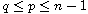 , we show
that compactness of the
, we show
that compactness of the
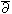 -Neumann operator,
-Neumann operator,
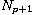 ,
on square integrable (0, p+1)-forms is equivalent to compactness of the
commutators
,
on square integrable (0, p+1)-forms is equivalent to compactness of the
commutators
![$[B_p,\overline z_j]$](images/ah.png) ,
,
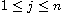 ,
on square integrable
,
on square integrable
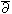 -closed (0, p)-forms, where
-closed (0, p)-forms, where
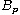 is the
Bergman projection on (0, p)-forms. Moreover, we prove that compactness of
the commutator of
is the
Bergman projection on (0, p)-forms. Moreover, we prove that compactness of
the commutator of
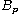 with bounded functions percolates up in the
with bounded functions percolates up in the
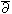 -complex on
-complex on
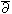 -closed forms and square
integrable holomorphic forms. Furthermore, we find a characterization of
compactness of the canonical solution operator,
-closed forms and square
integrable holomorphic forms. Furthermore, we find a characterization of
compactness of the canonical solution operator,
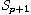 ,
of the
,
of the
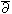 -equation restricted on (0, p+1)-forms
with holomorphic
coefficients in terms of compactness of commutators
-equation restricted on (0, p+1)-forms
with holomorphic
coefficients in terms of compactness of commutators
![$[T_p^{z_j*},T_p^{z_j}]$](images/am.png) ,
,
 ,
on (0, p)-forms with holomorphic coefficients,
where
,
on (0, p)-forms with holomorphic coefficients,
where
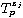 is the Bergman-Toeplitz operator acting on (0, p)-forms
with symbol
is the Bergman-Toeplitz operator acting on (0, p)-forms
with symbol
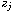 .
This extends to domains which are not necessarily
pseudoconvex.
.
This extends to domains which are not necessarily
pseudoconvex.
