Electron. J. Differential Equations,
Vol. 2018 (2018), No. 121, pp. 1-36.
Nonlinear parabolic-elliptic system in Musielak-Orlicz-Sobolev spaces
Francisco Ortegon Gallego, Mohamed Rhoudaf, Hajar Sabiki
Abstract:
The existence of a capacity solution to the thermistor problem in the
context of inhomogeneous Musielak-Orlicz-Sobolev spaces is analyzed.
This is a coupled parabolic-elliptic system of nonlinear PDEs whose
unknowns are the temperature inside a semiconductor material,
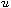 ,
and the electric potential,
,
and the electric potential,
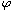 .
We study the general case where the nonlinear elliptic operator in the
parabolic equation is of the form
.
We study the general case where the nonlinear elliptic operator in the
parabolic equation is of the form
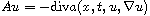 , A being a Leray-Lions operator
defined on
, A being a Leray-Lions operator
defined on
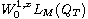 , where M is a generalized N-function.
, where M is a generalized N-function.
Submitted December 26, 2017. Published June 15, 2018.
Math Subject Classifications: 35J70, 35K61, 46E30, 35M13.
Key Words: Parabolic-elliptic system; Musielak-Orlicz-Sobolev spaces;
weak solutions; capacity solutions.
An addendum was posted on August 14, 2019. It corrects the proof of an inequality.
See the last two pages of this article.
Show me the PDF file (437 KB),
TEX file for this article.
 |
Francisco Ortegón Gallego
Departamento de Matemáticas
Facultad de Ciencias, Universidad de Cádiz
Campus del Río San Pedro
11510 Puerto Real, Cádiz, Spain
email: francisco.ortegon@uca.es
|
|---|
 |
Mohamed Rhoudaf
Faculté des Sciences de Meknès
Université Moulay-Ismaïl - Meknès
Équipe: EDPs et Calcul Scientifique, Marocco
email: rhoudafmohamed@gmail.com
|
|---|
 |
Hajar Sabiki
Laboratoire d'Analyse
Géométrie et Applications
Faculté des Sciences
BP 133 Kénitra 14000, Marocco
email: sabikihajar@gmail.com
|
|---|
Return to the EJDE web page
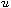 ,
and the electric potential,
,
and the electric potential,
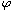 .
We study the general case where the nonlinear elliptic operator in the
parabolic equation is of the form
.
We study the general case where the nonlinear elliptic operator in the
parabolic equation is of the form
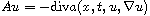 , A being a Leray-Lions operator
defined on
, A being a Leray-Lions operator
defined on
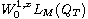 , where M is a generalized N-function.
, where M is a generalized N-function.


