Electron. J. Differential Equations,
Vol. 2018 (2018), No. 132, pp. 1-21.
Renormalized solutions for nonlinear parabolic equations with
general measure data
Mohammed Abdellaoui, Elhoussine Azroul
Abstract:
We prove the existence of parabolic initial boundary value problems of the type
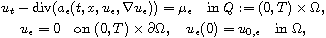
with respect to suitable convergence of the nonlinear operators
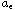 and of the measure data
and of the measure data
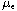 .
As a consequence, we obtain the existence of a renormalized solution
for a general class of nonlinear parabolic equations with right-hand
side measure.
.
As a consequence, we obtain the existence of a renormalized solution
for a general class of nonlinear parabolic equations with right-hand
side measure.
Submitted July 15, 2017. Published June 27, 2018.
Math Subject Classifications: 35R06, 41A30, 35B45, 37K45, 32U20.
Key Words: Nonlinear parabolic problems; p-capacity; renormalized solution;
stability; general measure.
Show me the PDF file (340 KB),
TEX file for this article.
 |
Mohammed Abdellaoui
University of Fez, Faculty of Sciences Dhar El Mahraz
Laboratory LAMA, Department of Mathematics, B.P. 1796
Atlas Fez, Morocco
email: mohammed.abdellaoui3@usmba.ac.ma
|
|---|
 |
Elhoussine Azroul
University of Fez, Faculty of Sciences Dhar El Mahraz
Laboratory LAMA, Department of Mathematics, B.P. 1796
Atlas Fez, Morocco
email: elhoussine.azroul@usmba.ac.ma
|
|---|
Return to the EJDE web page
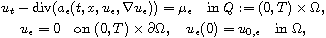
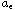 and of the measure data
and of the measure data
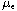 .
As a consequence, we obtain the existence of a renormalized solution
for a general class of nonlinear parabolic equations with right-hand
side measure.
.
As a consequence, we obtain the existence of a renormalized solution
for a general class of nonlinear parabolic equations with right-hand
side measure.

