Electron. J. Differential Equations,
Vol. 2018 (2018), No. 137, pp. 1-14.
Asymptotic behavior of positive solutions of a semilinear
Dirichlet problem in exterior domains
Habib Maagli, Abdulah Khamis Alzahrani, Zagharide Zine El Abidine
Abstract:
In this article, we study the existence, uniqueness and the asymptotic
behavior of a positive classical solution to the semilinear boundary
value problem
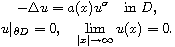
Here D is an unbounded regular domain in
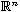 (
(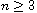 )
with compact boundary,
)
with compact boundary,
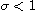 and the function a is a nonnegative
function in
and the function a is a nonnegative
function in
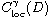 ,
,
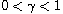 ,
satisfying an
appropriate assumption related to Karamata regular variation theory.
,
satisfying an
appropriate assumption related to Karamata regular variation theory.
Submitted September 20, 2017. Published July 1, 2018.
Math Subject Classifications: 34B16, 34B18, 35B09, 35B40.
Key Words: Positive solutions; asymptotic behavior; Dirichlet problem;
subsolution; supersolution.
Show me the PDF file (282 KB),
TEX file for this article.
 |
Habib Mâagli
King Abdulaziz University
College of Sciences and Arts, Rabigh Campus
Department of Mathematics. P. O. Box 344
Rabigh 21911, Saudi Arabia
email: habib.maagli@fst.rnu.tn
|
|---|
| |
Abdulah Khamis Alzahrani
King Abdulaziz University, Faculty of Sciences
Department of Mathematics. P. O. Box 80203
Jeddah 21589, Saudi Arabia
email: akalzahrani@kau.edu.sa
|
|---|
 |
Zagharide Zine El Abidine
Université de Tunis El Manar
Faculté des Sciences de Tunis
UR11ES22 Potentiels et Probabilités
2092 Tunis, Tunisie
email: Zagharide.Zinelabidine@ipeib.rnu.tn
|
|---|
Return to the EJDE web page
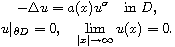
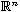 (
(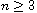 )
with compact boundary,
)
with compact boundary,
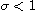 and the function a is a nonnegative
function in
and the function a is a nonnegative
function in
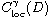 ,
,
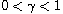 ,
satisfying an
appropriate assumption related to Karamata regular variation theory.
,
satisfying an
appropriate assumption related to Karamata regular variation theory.

