Electron. J. Differential Equations,
Vol. 2018 (2018), No. 144, pp. 1-19.
Existence of multiple solutions and estimates of extremal values
for a Kirchhoff type problem with fast increasing weight and
critical nonlinearity
Xiaotao Qian, Jianqing Chen
Abstract:
In this article, we study the Kirchhoff type problem
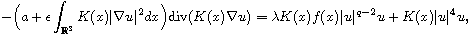
where
 ,
,
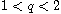 ,
,
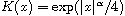 with
with
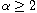 ,
,
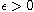 is small enough, and the parameters
is small enough, and the parameters
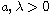 .
Under some assumptions on
.
Under some assumptions on
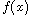 ,
we establish the existence of two nonnegative
nontrivial solutions and obtain uniform lower estimates for extremal values
of the problem via variational methods.
,
we establish the existence of two nonnegative
nontrivial solutions and obtain uniform lower estimates for extremal values
of the problem via variational methods.
Submitted February 10, 2018. Published July 17, 2018.
Math Subject Classifications: 35J20, 35J60.
Key Words: Variational methods; Kirchhoff type equation;
critical nonlinearity; multiple solutions; extremal values.
Show me the PDF file (302 KB),
TEX file for this article.
 |
Xiaotao Qian
College of Mathematics and Computer Science
& FJKLMAA, Fujian Normal University
Qishan Campus, Fuzhou 350108, China
email: qianxiaotao1984@163.com
|
|---|
 |
Jianqing Chen
College of Mathematics and Computer Science
& FJKLMAA, Fujian Normal University
Qishan Campus, Fuzhou 350108, China
email: jqchen@fjnu.edu.cn
|
|---|
Return to the EJDE web page
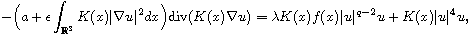
 ,
,
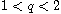 ,
,
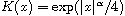 with
with
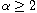 ,
,
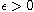 is small enough, and the parameters
is small enough, and the parameters
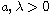 .
Under some assumptions on
.
Under some assumptions on
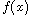 ,
we establish the existence of two nonnegative
nontrivial solutions and obtain uniform lower estimates for extremal values
of the problem via variational methods.
,
we establish the existence of two nonnegative
nontrivial solutions and obtain uniform lower estimates for extremal values
of the problem via variational methods.

