Electron. J. Differential Equations,
Vol. 2018 (2018), No. 147, pp. 1-15.
Existence of infinitely solutions for a modified nonlinear
Schrodinger equation via dual approach
Xinguang Zhang, Lishan Liu, Yonghong Wu, Yujun Cui
Abstract:
In this article, we focus on the existence of infinitely many weak solutions
for the modified nonlinear Schrodinger equation
![$$
-\Delta u+V(x) u-[\Delta(1+u^2)^{\alpha/2}]\frac{\alpha u}{2(1+u^2)
^{\frac{2-\alpha}2}}=f(x,u),\quad \text{in } \mathbb{R}^N,
$$](images/aa.png)
where
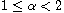 ,
,
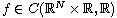 .
By using a symmetric mountain pass theorem and dual approach, we prove
that the above equation has infinitely many high energy solutions.
.
By using a symmetric mountain pass theorem and dual approach, we prove
that the above equation has infinitely many high energy solutions.
Submitted March 8, 2018. Published July 31, 2018.
Math Subject Classifications: 35J50, 35J92.
Key Words: Modified nonlinear Schrodinger equation; dual approach;
critical point theorem; multiplicity; variational methods.
Show me the PDF file (290 KB),
TEX file for this article.
 |
Xinguang Zhang
School of Mathematical and Informational Sciences
Yantai University
Yantai 264005, Shandong, China
email: xinguang.zhang@curtin.edu.au
|
|---|
 |
Lishan Liu
School of Mathematical Sciences
Qufu Normal University
Qufu 273165, Shandong, China
email: mathlls@163.com
|
|---|
 |
Yonghong Wu
Department of Mathematics and Statistics
Curtin University of Technology
Perth, WA 6845, Australia
email: y.wu@curtin.edu.au
|
|---|
 |
Yujun Cui
Department of Mathematics
Shandong University of Science and Technology
Qingdao, 266590, Shandong, China
email: cyj720201@163.com
|
|---|
Return to the EJDE web page
![$$
-\Delta u+V(x) u-[\Delta(1+u^2)^{\alpha/2}]\frac{\alpha u}{2(1+u^2)
^{\frac{2-\alpha}2}}=f(x,u),\quad \text{in } \mathbb{R}^N,
$$](images/aa.png)
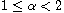 ,
,
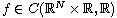 .
By using a symmetric mountain pass theorem and dual approach, we prove
that the above equation has infinitely many high energy solutions.
.
By using a symmetric mountain pass theorem and dual approach, we prove
that the above equation has infinitely many high energy solutions.



