Under consideration is the damped semilinear wave equation
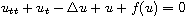
in a bounded domain
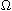 in
in
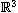 subject to an acoustic
boundary condition with a singular perturbation, which we term
"massless acoustic perturbation",
subject to an acoustic
boundary condition with a singular perturbation, which we term
"massless acoustic perturbation",
![$$
\varepsilon\delta_{tt}+\delta_t+\delta
= -u_t\quad\text{for}\quad \varepsilon\in[0,1].
$$](images/ad.png)
By adapting earlier work by Frigeri, we prove the existence of a family of global attractors for each
![$\varepsilon\in[0,1]$](images/ae.png) .
We also establish the optimal regularity for the global attractors, as well
as the existence of an exponential attractor, for each
.
We also establish the optimal regularity for the global attractors, as well
as the existence of an exponential attractor, for each
![$\varepsilon\in[0,1]$](images/ae.png) .
The later result insures the global attractors possess finite (fractal)
dimension, however, we cannot yet guarantee that this dimension is independent
of the perturbation parameter
.
The later result insures the global attractors possess finite (fractal)
dimension, however, we cannot yet guarantee that this dimension is independent
of the perturbation parameter
 .
The family of global attractors are upper-semicontinuous with respect to the
perturbation parameter
.
The family of global attractors are upper-semicontinuous with respect to the
perturbation parameter
 ;
a result which follows by an application
of a new abstract result also contained in this article.
Finally, we show that it is possible to obtain the global attractors using
weaker assumptions on the nonlinear term f, however, in that case,
the optimal regularity, the finite dimensionality, and the upper-semicontinuity
of the global attractors does not necessarily hold.
;
a result which follows by an application
of a new abstract result also contained in this article.
Finally, we show that it is possible to obtain the global attractors using
weaker assumptions on the nonlinear term f, however, in that case,
the optimal regularity, the finite dimensionality, and the upper-semicontinuity
of the global attractors does not necessarily hold.
