Electron. J. Differential Equations,
Vol. 2018 (2018), No. 153, pp. 1-18.
Bifurcation and multiplicity results for critical magnetic fractional problems
Alessio Fiscella, Eugenio Vecchi
Abstract:
This article concerns the bifurcation phenomena and the existence of multiple
solutions for a non-local boundary value problem driven by the magnetic
fractional Laplacian
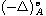 .
In particular, we consider
.
In particular, we consider
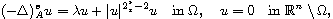
where
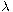 is a real parameter and
is a real parameter and
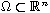 is an
open and bounded set with Lipschitz boundary.
is an
open and bounded set with Lipschitz boundary.
Submitted April 6, 2018. Published August 13, 2018.
Math Subject Classifications: 35R11, 35Q60, 35A15, 35B33.
Key Words: Fractional magnetic operators; critical nonlinearities;
variational methods.
Show me the PDF file (331 KB),
TEX file for this article.
 |
Alessio Fiscella
Departamento de Matemática
Universidade Estadual de Campinas, IMECC
Rua Sérgio Buarque de Holanda 651
Campinas, SP CEP 13083-859 Brazil
email: fiscella@ime.unicamp.br
|
|---|
 |
Eugenio Vecchi
Dipartimento di Matematica
Sapienza Universitá di Roma
P.le Aldo Moro 5, 00185, Roma, Italy
email: vecchi@mat.uniroma1.it
|
|---|
Return to the EJDE web page
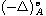 .
In particular, we consider
.
In particular, we consider
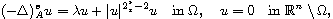
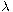 is a real parameter and
is a real parameter and
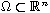 is an
open and bounded set with Lipschitz boundary.
is an
open and bounded set with Lipschitz boundary.

