Electron. J. Differential Equations,
Vol. 2018 (2018), No. 165, pp. 1-14.
Sharper estimates for the eigenvalues of the Dirichlet
fractional Laplacian on planar domains
Selma Yildirim, Turkay Yolcu
Abstract:
In this article, we study the eigenvalues of the
Dirichlet fractional Laplacian operator
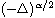 ,
,
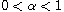 ,
restricted to a bounded planar domain
,
restricted to a bounded planar domain
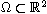 . We establish new sharper lower bounds
in the sense of the Weyl law for the of sums of eigenvalues,
which advance the recent results obtained in several articles even
in a more general setting.
. We establish new sharper lower bounds
in the sense of the Weyl law for the of sums of eigenvalues,
which advance the recent results obtained in several articles even
in a more general setting.
Submitted March 22, 2018. Published September 12, 2018.
Math Subject Classifications: 35P15, 35P20, 60G52.
Key Words: Fractional Laplacian; stable processes; eigenvalue.
Show me the PDF file (385 KB),
TEX file for this article.
 |
Selma Yildirim
The University of Chicago
Department of Mathematics
Chicago, IL 60637, USA
email: selma@uchicago.edu, selmayildirim@gmail.com
|
|---|
 |
Turkay Yolcu
Bradley University
Department of Mathematics
Peoria, IL 61625, USA
email: tyolcu@bradley.edu
|
|---|
Return to the EJDE web page
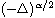 ,
,
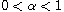 ,
restricted to a bounded planar domain
,
restricted to a bounded planar domain
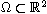 . We establish new sharper lower bounds
in the sense of the Weyl law for the of sums of eigenvalues,
which advance the recent results obtained in several articles even
in a more general setting.
. We establish new sharper lower bounds
in the sense of the Weyl law for the of sums of eigenvalues,
which advance the recent results obtained in several articles even
in a more general setting.

