We study the Heston model for pricing European options on stocks with stochastic volatility. This is a Black-Scholes-type equation whose spatial domain for the logarithmic stock price
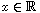 and the variance
and the variance
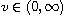 is the half-plane
is the half-plane
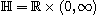 .
The volatility is then given by
.
The volatility is then given by
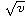 .
The diffusion equation for the price of the European call option
p = p(x,v,t) at time
.
The diffusion equation for the price of the European call option
p = p(x,v,t) at time
 is parabolic and degenerates at
the boundary
is parabolic and degenerates at
the boundary
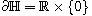 as
as
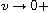 .
The goal is to hedge with this option against
volatility fluctuations, i.e., the function
.
The goal is to hedge with this option against
volatility fluctuations, i.e., the function
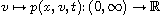 and its (local) inverse are of particular interest.
We prove that
and its (local) inverse are of particular interest.
We prove that
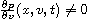 holds almost everywhere in
holds almost everywhere in
 by establishing the analyticity of p in both,
space (x,v) and time t variables.
To this end, we are able to show that the Black-Scholes-type operator,
which appears in the diffusion equation,
generates a holomorphic
by establishing the analyticity of p in both,
space (x,v) and time t variables.
To this end, we are able to show that the Black-Scholes-type operator,
which appears in the diffusion equation,
generates a holomorphic
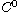 -semigroup
in a suitable weighted
-semigroup
in a suitable weighted
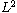 -space over
-space over
 .
We show that the
.
We show that the
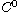 -semigroup
solution can be extended to
a holomorphic function in a complex domain in
-semigroup
solution can be extended to
a holomorphic function in a complex domain in
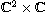 ,
by establishing some new a~priori weighted
,
by establishing some new a~priori weighted
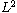 -estimates over
certain complex "shifts" of
-estimates over
certain complex "shifts" of
 for the unique holomorphic extension.
These estimates depend only on
the weighted
for the unique holomorphic extension.
These estimates depend only on
the weighted
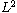 -norm
of the terminal data over
-norm
of the terminal data over
 (at t=T).
(at t=T).

