In this article, we consider the multiple solutions for the nonhomogeneous Choquard equations
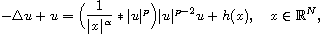
and
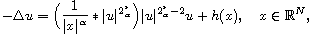
where
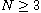 ,
,
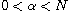 ,
,
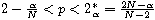 .
Under suitable assumptions on h, we obtain at least two solutions
on the subcritical case
.
Under suitable assumptions on h, we obtain at least two solutions
on the subcritical case
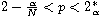 and on the critical case
and on the critical case
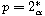 .
.
Lixia Wang
Abstract:
In this article, we consider the multiple solutions for the
nonhomogeneous Choquard equations
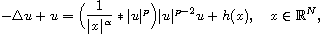
and
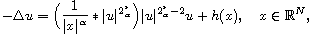
where
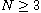 ,
,
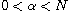 ,
,
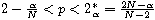 .
Under suitable assumptions on h, we obtain at least two solutions
on the subcritical case
.
Under suitable assumptions on h, we obtain at least two solutions
on the subcritical case
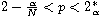 and on the critical case
and on the critical case
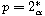 .
.
Submitted August 2, 2017. Published October 17, 2018.
Math Subject Classifications: 35J20, 35J60.
Key Words: Choquard equation; nonhomogeneous; critical exponent.
Show me the PDF file (351 KB), TEX file for this article.
 |
Lixia Wang School of Sciences Tianjin Chengjian University Tianjin 300384, China email: wanglixia0311@126.com |
|---|
Return to the EJDE web page