Electron. J. Differential Equations,
Vol. 2018 (2018), No. 184, pp. 1-23.
Center problem for generalized lambda-omega differential systems
Jaume Llibre, Rafael Ramirez, Valentin Ramirez
Abstract:
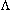 -
-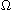 differential systems are the real planar
polynomial differential equations of degree m of the form
differential systems are the real planar
polynomial differential equations of degree m of the form
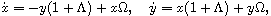
where
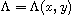 and
and
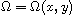 are polynomials of degree at most m-1 such that
are polynomials of degree at most m-1 such that
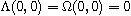 .
A planar vector field with linear type center can be written as a
.
A planar vector field with linear type center can be written as a
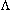 -
-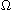 system if and only if the Poincare-Liapunov
first integral is of the form
system if and only if the Poincare-Liapunov
first integral is of the form
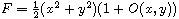 .
The main objective of this article is to study the center problem for
.
The main objective of this article is to study the center problem for
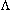 -
-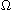 systems of degree m with
systems of degree m with
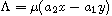 ,
and
,
and
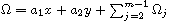 ,
where
,
where
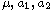 are constants and
are constants and
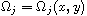 is a homogenous polynomial of degree
is a homogenous polynomial of degree
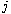 ,
for
,
for  .
We prove the following results. Assuming that
.
We prove the following results. Assuming that
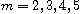 and
and
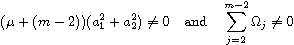
the
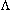 -
-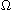 system has a weak center at the origin
if and only if these systems after a linear change of variables
system has a weak center at the origin
if and only if these systems after a linear change of variables
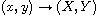 are invariant under the transformations
are invariant under the transformations
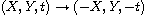 .
If
.
If
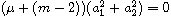 and
and
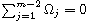 then the origin is a weak center. We observe that the main difficulty
in proving this result for m>6 is related to the huge computations.
then the origin is a weak center. We observe that the main difficulty
in proving this result for m>6 is related to the huge computations.
Submitted July 9, 2018. Published November 14, 2018.
Math Subject Classifications: 34C05, 34C07.
Key Words: Linear type center; Darboux first integral; weak center;
Poincare-Liapunov theorem; Reeb integrating factor.
Show me the PDF file (320 KB),
TEX file for this article.
 |
Jaume Llibre
Departament de Matemàtiques
Universitat Autònoma de Barcelona
08193 Bellaterra,
Barcelona, Catalonia, Spain
email: jllibre@mat.uab.cat
|
|---|
| |
Rafael Ramírez
Departament d'Enginyeria Informática i Matemátiques
Universitat Rovira i Virgili
Avinguda dels Pa&imul;sos Catalans 26
43007 Tarragona, Catalonia, Spain
email: rafaelorlando.ramirez@urv.cat
|
|---|
| |
Valentín Ramírez
Departament de Matemàtiques
Universitat Autònoma de Barcelona
08193 Bellaterra
Barcelona, Catalonia, Spain
email: valentin.ramirez@e-campus.uab.cat
|
|---|
Return to the EJDE web page
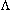 -
-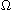 differential systems are the real planar
polynomial differential equations of degree m of the form
differential systems are the real planar
polynomial differential equations of degree m of the form
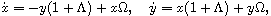
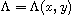 and
and
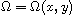 are polynomials of degree at most m-1 such that
are polynomials of degree at most m-1 such that
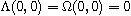 .
A planar vector field with linear type center can be written as a
.
A planar vector field with linear type center can be written as a
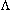 -
-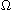 system if and only if the Poincare-Liapunov
first integral is of the form
system if and only if the Poincare-Liapunov
first integral is of the form
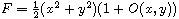 .
The main objective of this article is to study the center problem for
.
The main objective of this article is to study the center problem for
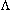 -
-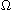 systems of degree m with
systems of degree m with
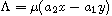 ,
and
,
and
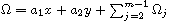 ,
where
,
where
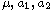 are constants and
are constants and
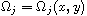 is a homogenous polynomial of degree
is a homogenous polynomial of degree
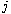 ,
for
,
for  .
We prove the following results. Assuming that
.
We prove the following results. Assuming that
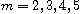 and
and
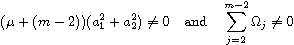
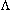 -
-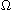 system has a weak center at the origin
if and only if these systems after a linear change of variables
system has a weak center at the origin
if and only if these systems after a linear change of variables
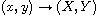 are invariant under the transformations
are invariant under the transformations
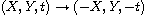 .
If
.
If
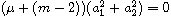 and
and
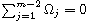 then the origin is a weak center. We observe that the main difficulty
in proving this result for m>6 is related to the huge computations.
then the origin is a weak center. We observe that the main difficulty
in proving this result for m>6 is related to the huge computations.
