Electron. J. Differential Equations,
Vol. 2018 (2018), No. 194, pp. 1-17.
Positive solution for Henon type equations with critical Sobolev growth
Kazune Takahashi
Abstract:
We investigate the Henon type equation involving the critical
Sobolev exponent with Dirichret boundary condition

in
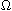 included in a unit ball, under several conditions.
Here,
included in a unit ball, under several conditions.
Here,
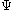 is a non-trivial given function with
is a non-trivial given function with
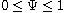 which may vanish on
which may vanish on
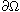 .
Let
.
Let
 be the first eigenvalue of the Dirichret eigenvalue problem
be the first eigenvalue of the Dirichret eigenvalue problem
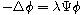 in
in
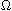 .
We show that if the dimension
.
We show that if the dimension
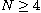 and
and
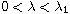 ,
there exists a positive solution for small
,
there exists a positive solution for small
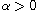 .
Our methods include the mountain pass theorem and the Talenti function.
.
Our methods include the mountain pass theorem and the Talenti function.
Submitted April 2, 2018. Published November 28, 2018.
Math Subject Classifications: 35J20, 35J60, 35J61, 35J91.
Key Words: Critical Sobolev exponent; Henon equation; mountain pass theorem;
Talenti function.
Show me the PDF file (279 KB),
TEX file for this article.
Kazune Takahashi
Graduate School of Mathematical Sciences
The University of Tokyo
3-8-1 Komaba Meguroku Tokyo 153-8914, Japan
email: kazunetakahashi@gmail.com
|
Return to the EJDE web page

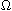 included in a unit ball, under several conditions.
Here,
included in a unit ball, under several conditions.
Here,
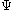 is a non-trivial given function with
is a non-trivial given function with
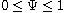 which may vanish on
which may vanish on
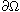 .
Let
.
Let
 be the first eigenvalue of the Dirichret eigenvalue problem
be the first eigenvalue of the Dirichret eigenvalue problem
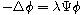 in
in
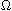 .
We show that if the dimension
.
We show that if the dimension
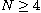 and
and
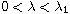 ,
there exists a positive solution for small
,
there exists a positive solution for small
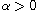 .
Our methods include the mountain pass theorem and the Talenti function.
.
Our methods include the mountain pass theorem and the Talenti function.