Electron. J. Differential Equations,
Vol. 2018 (2018), No. 28, pp. 1-11.
Logarithmic regularization of non-autonomous non-linear ill-posed problems
in Hilbert spaces
Matthew Fury
Abstract:
The regularization of non-autonomous non-linear ill-posed problems
is established using a logarithmic approximation originally proposed by
Boussetila and Rebbani, and later modified by Tuan and Trong.
We first prove continuous dependence on modeling where the solution of
the original ill-posed problem is estimated by the solution of an
approximate well-posed problem. Finally, we illustrate the convergence
via numerical experiments in
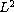 spaces.
spaces.
Submitted December 14, 2017. Published January 19, 2017.
Math Subject Classifications: 47D03, 35K91.
Key Words: Non-linear ill-posed problem; backward heat equation;
non-autonomous problem; semigroup of linear operators; regularization.
Show me the PDF file (251 KB),
TEX file for this article.
 |
Matthew Fury
Division of Science & Engineering
Penn State Abington
1600 Woodland Road,
Abington, PA 19001, USA
email: maf44@psu.edu
Tel 215-881-7553, Fax 215-881-7333
|
|---|
Return to the EJDE web page
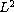 spaces.
spaces.
