Electron. J. Differential Equations,
Vol. 2018 (2018), No. 34, pp. 1-13.
Variational methods for Kirchhoff type problems with tempered fractional
derivative
Nemat Nyamoradi, Yong Zhou, Bashir Ahmad, Ahmed Alsaedi
Abstract:
In this article, using variational methods, we study the existence of solutions
for the Kirchhoff-type problem involving tempered fractional derivatives
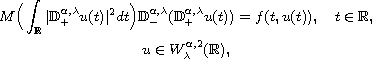
where
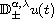 are the left and
right tempered fractional derivatives of order
are the left and
right tempered fractional derivatives of order
![$\alpha \in (1/2,1]$](gifs/ac.gif) ,
,
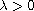 ,
,
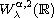 represent
the fractional Sobolev space,
represent
the fractional Sobolev space,
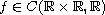 and
and
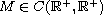 .
.
Submitted September 6, 2017. Published January 24, 2018.
Math Subject Classifications: 26A63, 34A38, 35A45.
Key Words: Tempered fractional calculus; Kirchhoff type problems;
Variational methods.
Show me the PDF file (286 KB),
TEX file for this article.
 |
Nemat Nyamoradi
Department of Mathematics
Faculty of Sciences
Razi University
Kermanshah 67149, Iran
email: neamat80@yahoo.com
|
|---|
 |
Yong Zhou
Faculty of Mathematics and Computational Science
Xiangtan University, Hunan 411105, China
email: yzhou@xtu.edu.cn
|
|---|
 |
Bashir Ahmad
Nonlinear Analysis and Applied Mathematics (NAAM) Research Group
Faculty of Science, King Abdulaziz University
Jeddah 21589, Saudi Arabia
email: bashirahmad_qau@yahoo.com
|
|---|
 |
Ahmed Alsaedi
Nonlinear Analysis and Applied Mathematics (NAAM) Research Group
Faculty of Science, King Abdulaziz University
Jeddah 21589, Saudi Arabia
email: aalsaedi@hotmail.com
|
|---|
Return to the EJDE web page
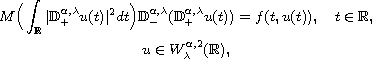
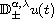 are the left and
right tempered fractional derivatives of order
are the left and
right tempered fractional derivatives of order
![$\alpha \in (1/2,1]$](gifs/ac.gif) ,
,
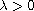 ,
,
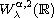 represent
the fractional Sobolev space,
represent
the fractional Sobolev space,
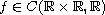 and
and
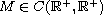 .
.



