Electron. J. Differential Equations,
Vol. 2018 (2018), No. 74, pp. 1-21.
First curve of Fucik spectrum for the p-fractional Laplacian
operator with nonlocal normal boundary conditions
Divya Goel, Sarika Goyal, Konijeti Sreenadh
Abstract:
In this article, we study the Fucik spectrum of the p-fractional
Laplace operator with nonlocal normal derivative conditions which
is defined as the set of all
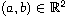 such that
such that

has a non-trivial solution u, where
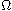 is a bounded domain in
is a bounded domain in
 with Lipschitz boundary,
with Lipschitz boundary,
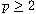 ,
,
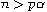 ,
,
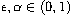 and
and
 .
We show existence of the first non-trivial curve
.
We show existence of the first non-trivial curve
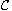 of the Fucik spectrum which is used to obtain the variational
characterization of a second eigenvalue of the problem defined above.
We also discuss some properties of this curve
of the Fucik spectrum which is used to obtain the variational
characterization of a second eigenvalue of the problem defined above.
We also discuss some properties of this curve
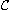 ,
e.g. Lipschitz continuous, strictly decreasing
and asymptotic behavior and non-resonance with respect to the
Fucik spectrum.
,
e.g. Lipschitz continuous, strictly decreasing
and asymptotic behavior and non-resonance with respect to the
Fucik spectrum.
Submitted November 22, 2017. Published March 17, 2018.
Math Subject Classifications: 35A15, 35J92, 35J60.
Key Words: Nonlocal operator; Fucik spectrum; Steklov problem; Non-resonance.
Show me the PDF file (408 KB),
TEX file for this article.
 |
Divya Goel
Department of Mathematics
Indian Institute of Technology Delhi
Hauz Khas, New Delhi-110016, India
email: divyagoel2511@gmail.com
|
|---|
 |
Sarika Goyal
Department of Mathematics
Bennett University, Greater Noida
Uttar Pradesh - 201310, India
email: sarika1.iitd@gmail.com
|
|---|
 |
Konijeti Sreenadh
Department of Mathematics
Indian Institute of Technology Delhi
Hauz Khaz, New Delhi-110016, India
email: sreenadh@maths.iitd.ac.in
|
|---|
Return to the EJDE web page
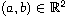 such that
such that

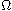 is a bounded domain in
is a bounded domain in
 with Lipschitz boundary,
with Lipschitz boundary,
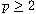 ,
,
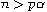 ,
,
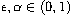 and
and
 .
We show existence of the first non-trivial curve
.
We show existence of the first non-trivial curve
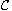 of the Fucik spectrum which is used to obtain the variational
characterization of a second eigenvalue of the problem defined above.
We also discuss some properties of this curve
of the Fucik spectrum which is used to obtain the variational
characterization of a second eigenvalue of the problem defined above.
We also discuss some properties of this curve
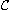 ,
e.g. Lipschitz continuous, strictly decreasing
and asymptotic behavior and non-resonance with respect to the
Fucik spectrum.
,
e.g. Lipschitz continuous, strictly decreasing
and asymptotic behavior and non-resonance with respect to the
Fucik spectrum.


