Electron. J. Differential Equations,
Vol. 2018 (2018), No. 92, pp. 1-14.
Positive solutions for the one-dimensional Sturm-Liouville
superlinear p-Laplacian problem
Khanh Duc Chu, Dang Dinh Hai
Abstract:
We prove the existence of positive classical solutions for the p-Laplacian
problem
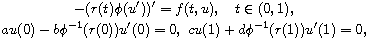
where
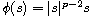 ,
,
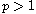 ,
,
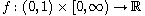 is a Caratheodory function satisfying
is a Caratheodory function satisfying
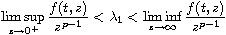
uniformly for a.e.
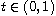 ,
where
,
where
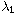 denotes the principal
eigenvalue of
denotes the principal
eigenvalue of
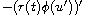 with Sturm-Liouville
boundary conditions. Our result extends a previous work by Manasevich,
Njoku, and Zanolin to the Sturm-Liouville boundary conditions with more
general operator.
with Sturm-Liouville
boundary conditions. Our result extends a previous work by Manasevich,
Njoku, and Zanolin to the Sturm-Liouville boundary conditions with more
general operator.
Submitted February 12, 2018. Published April 17, 2018.
Math Subject Classifications: 34B15, 34B18.
Key Words: p-Laplacian; superlinear; positive solutions.
Show me the PDF file (270 KB),
TEX file for this article.
 |
Khanh Duc Chu
Faculty of Mathematics and Statistics
Ton Duc Thang University
Ho chi Minh City, Vietnam
email: chuduckhanh@tdt.edu.vn
|
|---|
 |
Dang Dinh Hai
Department of Mathematics and Statistics
Mississippi state University
Mississippi State, MS 39762, USA
email: dang@math.msstate.edu
|
|---|
Return to the EJDE web page
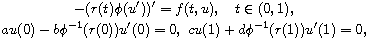
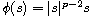 ,
,
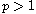 ,
,
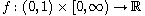 is a Caratheodory function satisfying
is a Caratheodory function satisfying
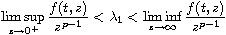
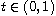 ,
where
,
where
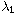 denotes the principal
eigenvalue of
denotes the principal
eigenvalue of
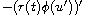 with Sturm-Liouville
boundary conditions. Our result extends a previous work by Manasevich,
Njoku, and Zanolin to the Sturm-Liouville boundary conditions with more
general operator.
with Sturm-Liouville
boundary conditions. Our result extends a previous work by Manasevich,
Njoku, and Zanolin to the Sturm-Liouville boundary conditions with more
general operator.

