Electron. J. Differential Equations,
Vol. 2018 (2018), No. 99, pp. 1-9.
Existence of solutions to biharmonic equations with sign-changing coefficients
Somayeh Saiedinezhad
Abstract:
In this article, we study the existence of solutions for the semi-linear
elliptic equation
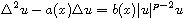
with Navier boundary condition
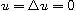 on
on
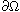 ,
where
,
where
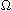 is a bounded domain with smooth boundary and
is a bounded domain with smooth boundary and
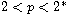 .
We consider two different assumptions on the potentials
.
We consider two different assumptions on the potentials
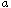 and
and
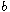 ,
including the case of sign-changing weights.
The approach is based on the Nehari manifold with variational arguments
about the corresponding fibering map, which ensures the multiple results.
,
including the case of sign-changing weights.
The approach is based on the Nehari manifold with variational arguments
about the corresponding fibering map, which ensures the multiple results.
Submitted July 17, 2017. Published Aapril 28, 2018.
Math Subject Classifications: 35A01, 35J35, 35D30, 35J91.
Key Words: Bi-Laplacian operator; weak solution; Nehari manifold; fibering map.
Show me the PDF file (225 KB),
TEX file for this article.
 |
Somayeh Saiedinezhad
School of Mathematics
Iran University of Science and Technology
Narmak, Tehran, Iran
email: ssaiedinezhad@iust.ac.ir
|
|---|
Return to the EJDE web page
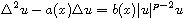
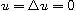 on
on
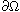 ,
where
,
where
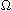 is a bounded domain with smooth boundary and
is a bounded domain with smooth boundary and
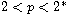 .
We consider two different assumptions on the potentials
.
We consider two different assumptions on the potentials
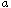 and
and
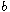 ,
including the case of sign-changing weights.
The approach is based on the Nehari manifold with variational arguments
about the corresponding fibering map, which ensures the multiple results.
,
including the case of sign-changing weights.
The approach is based on the Nehari manifold with variational arguments
about the corresponding fibering map, which ensures the multiple results.
