Electron. J. Differential Equations,
Vol. 2019 (2019), No. 102, pp. 1-16.
Non-trivial solutions of fractional Schrodinger-Poisson systems
with sum of periodic and vanishing potentials
Mingzhu Yu, Haibo Chen
Abstract:
We consider the fractional Schrodinger-Poisson system
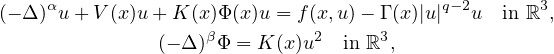
where
![$\alpha,\beta\in(0,1]$](images/a1x.png) ,
,
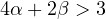 ,
,
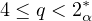 ,
K(x),
,
K(x),
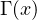 and f(x,u) are periodic in x, V is coercive or
and f(x,u) are periodic in x, V is coercive or
 is a sum of a periodic potential
is a sum of a periodic potential
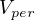 and a localized potential
and a localized potential
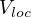 .
If f has the subcritical growth,
but higher than
.
If f has the subcritical growth,
but higher than
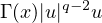 ,
we establish the existence and
nonexistence of ground state solutions are dependent on the sign of
,
we establish the existence and
nonexistence of ground state solutions are dependent on the sign of
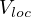 .
Moreover, we prove that such a problem admits infinitely many pairs of
geometrically distinct solutions provided that V is periodic and f
is odd in u. Finally, we investigate the existence of ground state solutions
in the case of coercive potential V.
.
Moreover, we prove that such a problem admits infinitely many pairs of
geometrically distinct solutions provided that V is periodic and f
is odd in u. Finally, we investigate the existence of ground state solutions
in the case of coercive potential V.
Submitted March 22, 2018. Published September 4, 2019.
Math Subject Classifications: 35B38, 35G99.
Key Words: Fractional Schrodinger-Poisson system; coercive potential;
periodic and localized potential; Nehari manifold; variational method.
Show me the PDF file (384 KB),
TEX file for this article.
 |
Mingzhu Yu
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: yumz_math@csu.edu.cn
|
|---|
 |
Haibo Chen
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: math_chb@163.com
|
|---|
Return to the EJDE web page
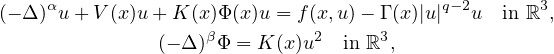
![$\alpha,\beta\in(0,1]$](images/a1x.png) ,
,
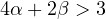 ,
,
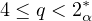 ,
K(x),
,
K(x),
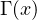 and f(x,u) are periodic in x, V is coercive or
and f(x,u) are periodic in x, V is coercive or
 is a sum of a periodic potential
is a sum of a periodic potential
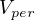 and a localized potential
and a localized potential
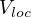 .
If f has the subcritical growth,
but higher than
.
If f has the subcritical growth,
but higher than
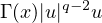 ,
we establish the existence and
nonexistence of ground state solutions are dependent on the sign of
,
we establish the existence and
nonexistence of ground state solutions are dependent on the sign of
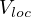 .
Moreover, we prove that such a problem admits infinitely many pairs of
geometrically distinct solutions provided that V is periodic and f
is odd in u. Finally, we investigate the existence of ground state solutions
in the case of coercive potential V.
.
Moreover, we prove that such a problem admits infinitely many pairs of
geometrically distinct solutions provided that V is periodic and f
is odd in u. Finally, we investigate the existence of ground state solutions
in the case of coercive potential V.

