Electron. J. Differential Equations,
Vol. 2019 (2019), No. 106, pp. 1-26.
Lagrangian structure for compressible flow in the half-space with
Navier boundary condition
Marcelo M. Santos, Edson J. Teixeira
Abstract:
We show the uniqueness of particle paths of a velocity field, which solves the
compressible isentropic Navier-Stokes equations in the half-space
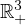 with the Navier boundary condition. More precisely,
by energy estimates and the assumption of small energy we prove that the velocity
field satisfies regularity estimates which imply the uniqueness of particle paths.
with the Navier boundary condition. More precisely,
by energy estimates and the assumption of small energy we prove that the velocity
field satisfies regularity estimates which imply the uniqueness of particle paths.
Submitted March 5, 2019. Published September 18, 2019.
Math Subject Classifications: 35Q30, 76N10, 35Q35, 35B99.
Key Words: Navier-Stokes equations; Lagrangian structure; Navier boundary condition.
Show me the PDF file (406 KB),
TEX file for this article.
| |
Marcelo M. Santos
Departamento de Matemática, IMECC-UNICAMP
Universidade Estadual de Campinas
Rua Sérgio Buarque de Holanda, 651
13083-859 - Campinas - SP, Brazil
email: msantos@ime.unicamp.br
|
|---|
 |
Edson J. Teixeira
Departamento de Matemática
UFV (Universidade Federal de Viçosa)
Av. PH. Rolfs, s/n,
36570-900 - Viçosa - MG, Brazil
email: edson.teixeira@ufv.br
|
|---|
Return to the EJDE web page
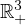 with the Navier boundary condition. More precisely,
by energy estimates and the assumption of small energy we prove that the velocity
field satisfies regularity estimates which imply the uniqueness of particle paths.
with the Navier boundary condition. More precisely,
by energy estimates and the assumption of small energy we prove that the velocity
field satisfies regularity estimates which imply the uniqueness of particle paths.
