Electron. J. Differential Equations,
Vol. 2019 (2019), No. 110, pp. 1-13.
Existence of a unique solution to an elliptic partial
differential equation
Diane L. Denny
Abstract:
The purpose of this article is to prove the existence of a unique
classical solution to the quasilinear elliptic
equation
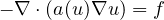 for
for
 ,
which satisfies the condition that
,
which satisfies the condition that
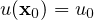 at a given point
at a given point
 ,
under the boundary condition
,
under the boundary condition
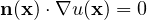 for
for
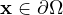 where
where
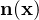 is the outward unit normal vector
and where
is the outward unit normal vector
and where
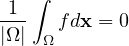 .
The domain
.
The domain
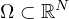 is a bounded, connected,
open set with a smooth boundary, and N=2 or N=3. The key to
the proof lies in obtaining a priori estimates for the solution.
is a bounded, connected,
open set with a smooth boundary, and N=2 or N=3. The key to
the proof lies in obtaining a priori estimates for the solution.
Submitted February 24, 2018. Published September 26, 2019.
Math Subject Classifications: 35A05
Key Words: Existence; uniqueness; quasilinear; elliptic.
Show me the PDF file (350 KB),
TEX file for this article.
 |
Diane L. Denny
Department of Mathematics and Statistics
Texas A&M University - Corpus Christi
Corpus Christi, TX 78412, USA
email: diane.denny@tamucc.edu
|
|---|
Return to the EJDE web page
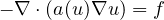 for
for
 ,
which satisfies the condition that
,
which satisfies the condition that
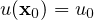 at a given point
at a given point
 ,
under the boundary condition
,
under the boundary condition
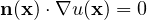 for
for
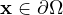 where
where
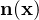 is the outward unit normal vector
and where
is the outward unit normal vector
and where
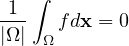 .
The domain
.
The domain
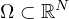 is a bounded, connected,
open set with a smooth boundary, and N=2 or N=3. The key to
the proof lies in obtaining a priori estimates for the solution.
is a bounded, connected,
open set with a smooth boundary, and N=2 or N=3. The key to
the proof lies in obtaining a priori estimates for the solution.
