Electron. J. Differential Equations, Vol. 2019 (2019), No. 113, pp. 1-21.

Slow motion for one-dimensional nonlinear damped hyperbolic Allen-Cahn systems

Raffaele Folino

Abstract:
We consider a nonlinear damped hyperbolic reaction-diffusion system in a bounded interval of the real line with homogeneous Neumann boundary conditions and we study the metastable dynamics of the solutions. Using an "energy approach" introduced by Bronsard and Kohn [11] to study slow motion for Allen-Cahn equation and improved by Grant [25] in the study of Cahn-Morral systems, we improve and extend to the case of systems the results valid for the hyperbolic Allen-Cahn equation (see [18]). 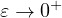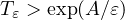In particular, we study the limiting behavior of the solutions as $\varepsilon\to 0^+$ , where $\varepsilon^2$ is the diffusion coefficient, and we prove existence and persistence of metastable states for a time $T_\varepsilon>\exp(A/\varepsilon)$. Such metastable states have a transition layer structure and the transition layers move with exponentially small velocity.

Submitted March 30, 2019. Published October 2, 2019.
Math Subject Classifications: 35L53, 35B25, 35K57.
Key Words: Hyperbolic reaction-diffusion systems; Allen-Cahn equation; metastability; energy estimates.

Show me the PDF file (413 KB), TEX file for this article.

Raffaele Folino
Dipartimento di Ingegneria e Scienze dell'Informazione e Matematica
Università degli Studi dell'Aquila
Italy
email: raffaele.folino@univaq.it

Return to the EJDE web page