Electron. J. Differential Equations,
Vol. 2019 (2019), No. 115, pp. 1-13.
Optimal bilinear control for Gross-Pitaevskii equations with singular potentials
Kai Wang, Dun Zhao
Abstract:
We study the optimal bilinear control problem of the generalized
Gross-Pitaevskii equation
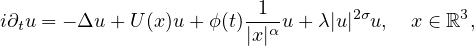
where U(x) is the given external potential,
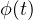 is the control function.
The existence of an optimal control and the optimality condition are presented
for suitable
is the control function.
The existence of an optimal control and the optimality condition are presented
for suitable
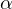 and
and
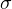 .
In particular, when
.
In particular, when
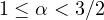 ,
the Frechet-differentiability of the objective functional is proved for
two cases:
(i)
,
the Frechet-differentiability of the objective functional is proved for
two cases:
(i)
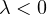 ,
,
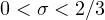 ;
(ii)
;
(ii)
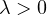 ,
,
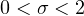 .
Comparing with the previous studies in [6], the results fill the gap for
.
Comparing with the previous studies in [6], the results fill the gap for
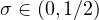 .
.
Submitted February 10, 2019. Published October 13, 2019.
Math Subject Classifications: 35Q55, 49J20.
Key Words: Optimal bilinear control; Gross-Pitaevskii equation; objective functional;
Frechet-differentiability; optimal condition.
Show me the PDF file (354 KB),
TEX file for this article.
 |
Kai Wang
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: wkai558@163.com
|
|---|
 |
Dun Zhao
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: zhaod@lzu.edu.cn
|
|---|
Return to the EJDE web page
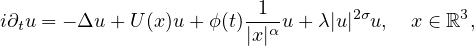
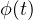 is the control function.
The existence of an optimal control and the optimality condition are presented
for suitable
is the control function.
The existence of an optimal control and the optimality condition are presented
for suitable
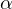 and
and
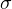 .
In particular, when
.
In particular, when
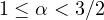 ,
the Frechet-differentiability of the objective functional is proved for
two cases:
(i)
,
the Frechet-differentiability of the objective functional is proved for
two cases:
(i)
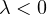 ,
,
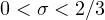 ;
(ii)
;
(ii)
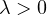 ,
,
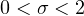 .
Comparing with the previous studies in [6], the results fill the gap for
.
Comparing with the previous studies in [6], the results fill the gap for
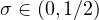 .
.

