We consider initial value problems for Caputo fractional equations of the form
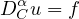 where f can have a singularity.
We consider all orders and prove equivalences with Volterra integral equations in
classical spaces such as
where f can have a singularity.
We consider all orders and prove equivalences with Volterra integral equations in
classical spaces such as
![$C^{m}[0,T]$](images/a1x.png) .
In particular for the case
.
In particular for the case
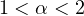 we consider nonlinearities of the form
we consider nonlinearities of the form
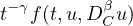 where
where
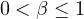 and
and
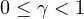 with f continuous, and we prove results on
existence of global
with f continuous, and we prove results on
existence of global
 solutions under linear growth assumptions on f(t,u,p)
in the u,p variables. With a Lipschitz condition we prove continuous dependence
on the initial data and uniqueness. One tool we use is a Gronwall inequality for
weakly singular problems with double singularities. We also prove some regularity
results and discuss monotonicity and concavity properties.
solutions under linear growth assumptions on f(t,u,p)
in the u,p variables. With a Lipschitz condition we prove continuous dependence
on the initial data and uniqueness. One tool we use is a Gronwall inequality for
weakly singular problems with double singularities. We also prove some regularity
results and discuss monotonicity and concavity properties.
