Electron. J. Differential Equations,
Vol. 2019 (2019), No. 18, pp. 1-16.
Multiple solutions for discontinuous elliptic problems involving
the fractional Laplacian
Jung-Hyun Bae, Yun-Ho Kim
Abstract:
In this article, we establish the existence of three weak solutions
for elliptic equations associated to the fractional Laplacian
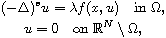
where
 is an open bounded subset in
is an open bounded subset in
 with Lipschitz boundary,
with Lipschitz boundary,
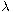 is a real parameter,
0<s<1, N>2s, and
is a real parameter,
0<s<1, N>2s, and
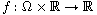 is measurable
with respect to each variable separately. The main purpose of this paper
is concretely to provide an estimate of the positive interval of the
parameters
is measurable
with respect to each variable separately. The main purpose of this paper
is concretely to provide an estimate of the positive interval of the
parameters
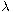 for which the problem above with discontinuous
nonlinearities admits at least three nontrivial weak solutions by applying
two recent three-critical-points theorems.
for which the problem above with discontinuous
nonlinearities admits at least three nontrivial weak solutions by applying
two recent three-critical-points theorems.
Submitted April 26, 2018. Published January 30, 2019.
Math Subject Classifications: 58E30, 49J52, 58E05.
Key Words: Fractional Laplacian; three-critical-points theorem;
multiple solutions.
Show me the PDF file (284 KB),
TEX file for this article.
Jung-Hyun Bae
Department of Mathematics
Sungkyunkwan University
Suwon 16419, Korea
email: hoi1000sa@skku.edu
|
Yun-Ho Kim
Department of Mathematics Education
Sangmyung University
Seoul 03016, Korea
email: kyh1213@smu.ac.kr
|
Return to the EJDE web page
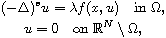
 is an open bounded subset in
is an open bounded subset in
 with Lipschitz boundary,
with Lipschitz boundary,
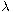 is a real parameter,
0<s<1, N>2s, and
is a real parameter,
0<s<1, N>2s, and
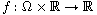 is measurable
with respect to each variable separately. The main purpose of this paper
is concretely to provide an estimate of the positive interval of the
parameters
is measurable
with respect to each variable separately. The main purpose of this paper
is concretely to provide an estimate of the positive interval of the
parameters
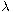 for which the problem above with discontinuous
nonlinearities admits at least three nontrivial weak solutions by applying
two recent three-critical-points theorems.
for which the problem above with discontinuous
nonlinearities admits at least three nontrivial weak solutions by applying
two recent three-critical-points theorems.